指数関数
指数関数は,
\(\Large \displaystyle y_i = a_0 \ Exp (- a_1 x_i) \)
とします.実際に適当な指数関数を作ってみます.
| i | x | y |
| 1 | 0 | 10 |
| 2 | 2 | 4 |
| 3 | 3 | 2 |
| 4 | 4 | 1 |
| 5 | 6 | 0.5 |
| 6 | 9 | 0.1 |
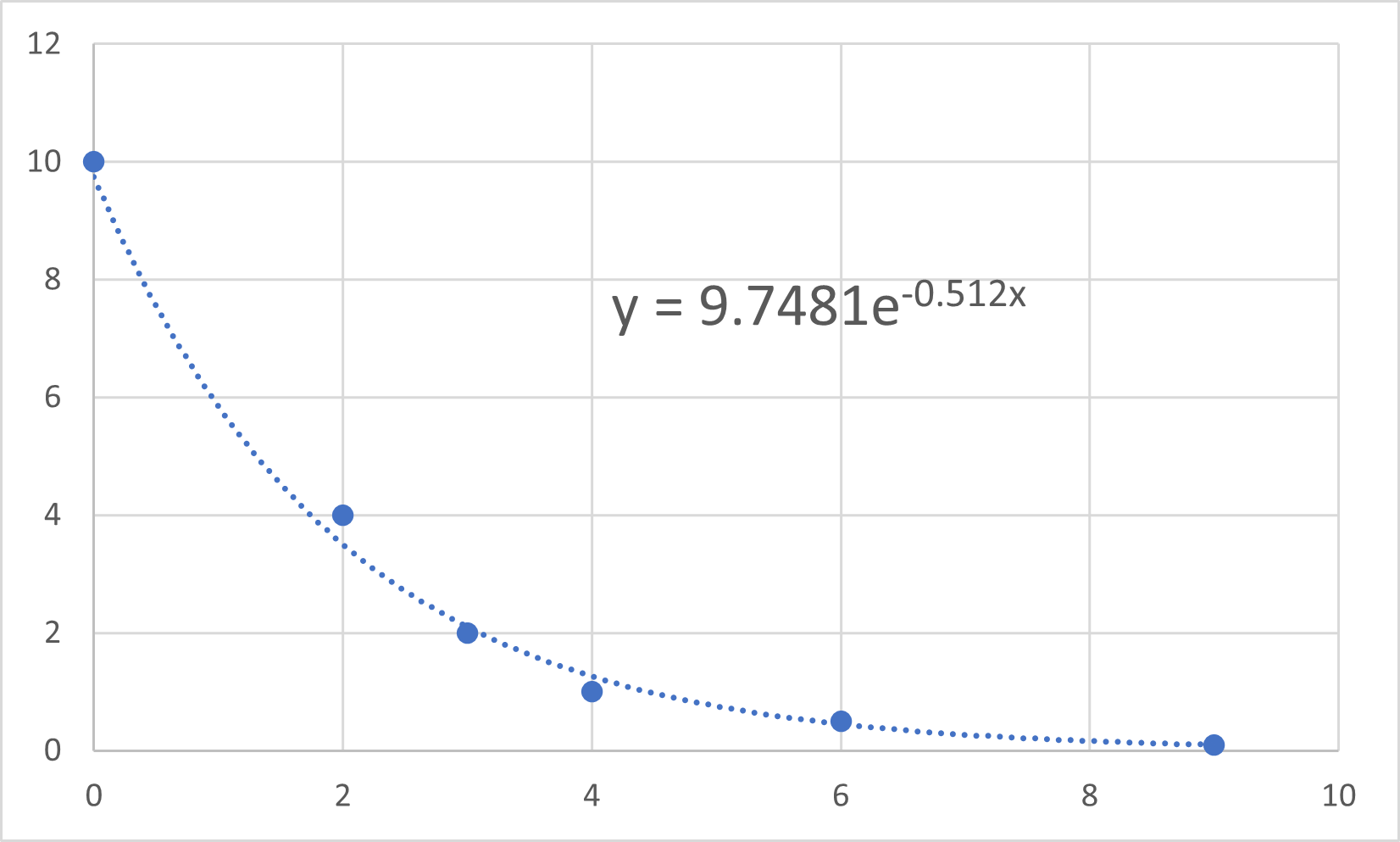
グラフ化すると,

となり,エクセルの近似曲線(指数近似)でフィットできます.
しかし,エクセル内では,縦軸を対数にしてから直線近似しているので,データそのままの近似の結果と異なります.
実際に対数に変換しないで,ソルバーをかけてみると,
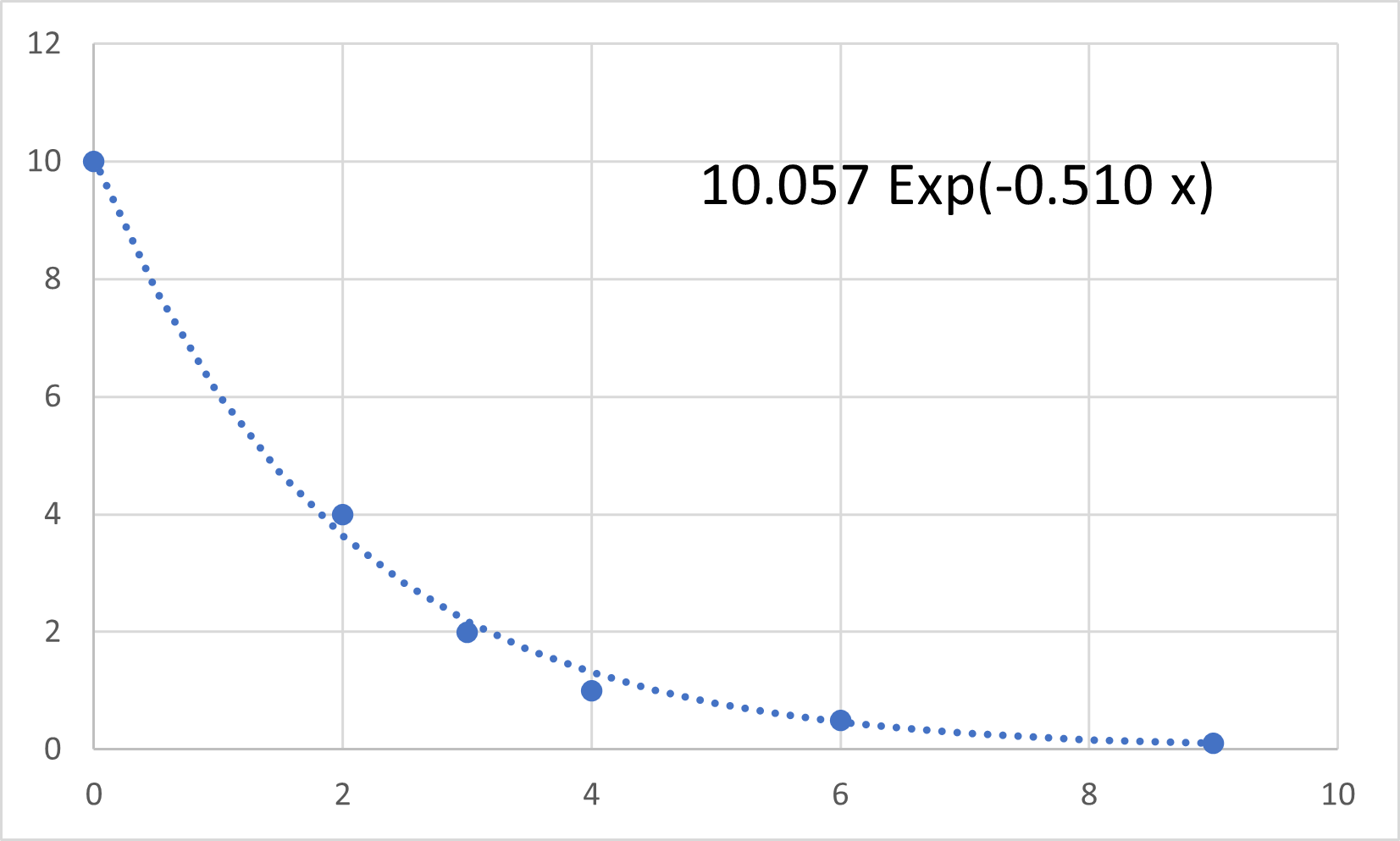
となります.
結果は,
\(\Large \displaystyle a_0 = 10.057 \)
\(\Large \displaystyle a_1 = 0.510 \)
となりました.
残差の平方和を計算すると,
| i | x | y | \( \hat{y} \) |
| 1 | 0 | 10 | 10.05689 |
| 2 | 2 | 4 | 3.627404 |
| 3 | 3 | 2 | 2.178522 |
| 4 | 4 | 1 | 1.308363 |
| 5 | 6 | 0.5 | 0.471911 |
| 6 | 9 | 0.1 | 0.102225 |
| Se (\(y_i - \hat{y} \)の平方和) | 0.269816 |
と計算できます.ここで,
自由度 : n-2 = 4
となりますので,
・分散
\(\Large \displaystyle Ve = = \frac{Se}{n-2} = \frac{0.269816}{6-2} = 0.067454 \)
となります.
次に,各パラメータをシフトさせて残差の平方和がどう変化するかを見ていきましょう.